Brøk. Multiplikasjon av brøkdeler av vanlig, desimal, blandet

I løpet av mellom- og videregående skoleeleverpasserte temaet "Fraksjoner". Dette konseptet er imidlertid mye bredere enn det som er gitt i læringsprosessen. I dag forekommer begrepet en brøk ganske ofte, og ikke alle kan beregne noe uttrykk, for eksempel multiplisere brøker.

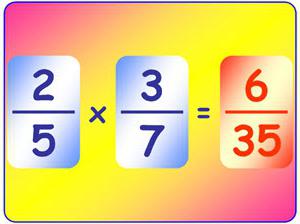
Hva er en brøkdel?

Så historisk, brøkdelte talldukket opp på grunn av behovet for å måle. Som praksis viser, er det ofte eksempler på å bestemme lengden på et segment, volumet av en rektangulær parallellpiped, et rektangelområde.

I utgangspunktet blir studentene kjent med slikekonsept, som en del. For eksempel, hvis du deler en vannmelon i 8 deler, så vil hver få en åttende vannmelon. Denne delen av de åtte kalles aksjen.

En andel som er ½ av en hvilken som helst verdi kalles en halv; ⅓ - den tredje; ¼ - en kvart. Rekord av skjemaet ⁵/₈, ⁴/₅, ²/₄ kalles vanlige fraksjoner. Ordinær fraksjon er delt inn i teller og nevner. Mellom dem er en funksjon av brøkdelen, eller en brøkdel. En brøklinje kan tegnes som en horisontal eller skrå linje. I dette tilfellet betegner det divisjonsskiltet.

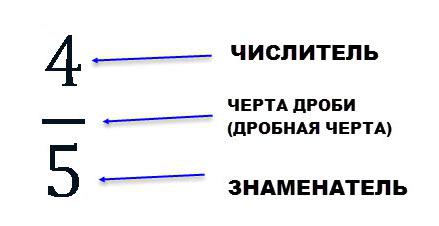
Nevneren representerer hvor mange like deler en kvantitet er delt av et objekt; og telleren - hvor mange identiske aksjer er tatt. Telleren er skrevet over brøklinjen, nevnen er skrevet under den.

Det er mest praktisk å vise vanlige fraksjoner påkoordinat stråle. Hvis et enkelt segment er delt inn i 4 like deler, betegne hver del med et latinsk brev, så kan du få et utmerket visuelt hjelpemiddel. Således viser punkt A en brøkdel som er lik ¹/₄ fra hele enhetsintervallet og punkt B-merkene ²/₈ av dette segmentet.

Variasjon av fraksjoner

Fraksjoner er vanlige, desimaltall og også blandede tall. I tillegg kan fraksjoner deles inn i vanlig og uregelmessig. Denne klassifiseringen er mer egnet for vanlige fraksjoner.

En korrekt brøkdel er et nummer hvisTelleren er mindre enn nevneren. Følgelig er det uekte brøk - et tall som har mer enn telleren nevneren. Den andre typen er vanligvis skrevet i form av et blandet nummer. Dette uttrykket består av et heltall og en brøkdel. For eksempel 1½. 1 - heltalldel, ½ - brøkdel. Men hvis du trenger å utføre enhver manipulasjon av uttrykket (divisjon eller multiplikasjon av brøker og deres reduksjon eller konvertering), er blandet tall oversatt til uekte brøk.

Det korrekte fraksjonelle uttrykket er alltid mindre enn ett, og det ukorrekte fraksjonelle uttrykket er større enn eller lik 1.

Som for decimaler, detteuttrykk betyr en post der et hvilket som helst tall er representert, nevneren av et brøk uttrykk som kan uttrykkes i form av en enhet med flere nuller. Hvis fraksjonen er riktig, vil heltalldelen i desimalnoteringen være null.

For å registrere et desimal må du førstskriv hele delen, skille den fra en brøkdel med et komma og skriv deretter et brøk uttrykk. Det skal huskes at telleren etter et komma må inneholde så mange numeriske tegn som nullene i nevnen.

eksempel. Presentere en brøkdel av 7²¹/₁₀₀₀ i desimalnotasjonen.

Algoritmen for å konvertere en uregelmessig brøkdel til et blandet tall og omvendt

For å registrere feil fraksjon i svaret på problemet er feil, må det derfor oversettes til et blandet nummer:

• å dele telleren av eksisterende nevner
• i et spesielt eksempel er et ufullstendig kvotient et heltall;
• og resten er telleren av fraksjonen, og nevneren forblir uendret.

eksempel. Oversett feil fraksjon til et blandet nummer: ⁴⁷/₅.

Løsningen. 47: 5. En ufullstendig kvotient er lik 9, en rest = 2. Derfor, ⁴⁷/₅ = 9²/₅.

Noen ganger er det nødvendig å presentere et blandet tall som en uregelmessig fraksjon. Deretter må du bruke følgende algoritme:

• hele delen multipliseres med nevneren av fraksjonalt uttrykk;
• Det resulterende produkt blir lagt til telleren;
• Resultatet er skrevet i telleren, nevneren forblir uendret.

eksempel. Represent nummeret i en blandet form som en uregelmessig fraksjon: 9⁸/₁₀.

Løsningen. 9 x 10 + 8 = 90 + 8 = 98 er telleren.

svaret: ⁹⁸/_10.

Multiplikasjon av brøkdeler av vanlig

Over vanlige fraksjoner kan gjøresulike algebraiske operasjoner. For å multiplisere to tall, må telleren multipliseres med telleren, og nevneren med nevneren. Og multiplikasjon av fraksjoner med forskjellige betegnelser adskiller seg ikke fra produktet av brøkdelte tall med samme betegnelser.

Det skjer at etter å finne resultatet du trengerklipp fraksjonen. Det er absolutt nødvendig å forenkle det resulterende uttrykket så mye som mulig. Selvfølgelig kan vi ikke si at feil fraksjon i svaret er en feil, men det er også vanskelig å kalle et riktig svar på det.

eksempel. Finn produktet av to vanlige fraksjoner: ½ og ²⁰/₁₈.

Som det fremgår av eksemplet, ble det oppnådd en reduksjonsfraksjon som ble funnet etter å ha funnet produktet. Både teller og nevner i dette tilfellet er delt med 4, og resultatet er svaret ⁵/₉.

Multiplikasjon av desimaler

Produktet av desimalt brøkdeler avviker ganske mye fra produktet av vanlige på sin egen måte. Således er multiplikasjonen av fraksjoner som følger:

• to desimaler som skal skrives under hver annen, slik at sifrene lengst til høyre var den ene over den andre;
• Det er nødvendig å multiplisere registrerte tall, til tross for komma, det vil si som naturlige tall;
• Beregn antall sifre etter desimaltegnet i hvert av tallene;
• i det resulterende resultatet etter å multiplisere resultatet, er det nødvendig å telle ut så mange numeriske symboler som det er i summen i begge faktorene etter kommaet, og sett separasjonsskiltet;
• Hvis tallene i produktet var mindre, så før de må du skrive så mange nuller som dekker dette tallet, legg et komma og tilordne hele delen lik null.

eksempel. Beregn produktet med to desimaltall: 2,25 og 3,6.

Løsningen.

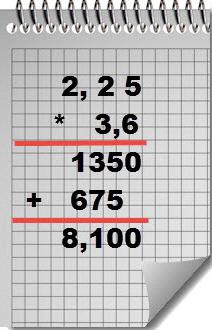
Multiplikasjon av blandede fraksjoner

For å beregne produktet av to blandede fraksjoner, må vi bruke multiplikasjonsregelen:

• oversette tall i blandet form til uregelmessige fraksjoner;
• finn produktet av tellerne;
• finn produktet av denominators;
• ta opp resultatet
• for å forenkle uttrykket så mye som mulig.

eksempel. Finn produktet 4 1 og 6²/_5.

Multiplikasjon av et tall med en brøkdel (brøker med et tall)

I tillegg til å finne produktet av to fraksjoner, blandede tall, er det jobber hvor det er nødvendig å multiplisere det naturlige tallet med en brøkdel.

Så, for å finne produktet med en desimalfraksjon og et naturlig tall, trenger du:

• skriv tallet under fraksjonen slik at de høyeste sifrene er over den andre;
• finn produktet, til tross for komma;
• i det resulterende resultatet, for å skille hele delen fra brøkdel med et komma, teller tallet i tallet etter desimaltegnet i brøkdelen.

For å formere en vanlig fraksjon med et tall, er det nødvendig å finne produktet av telleren og den naturlige faktoren. Hvis svaret er en reduksjonsfraksjon, bør den konverteres.

eksempel. Beregn produktet ⁵/₈ og 12.

Løsningen. ⁵/₈ * 12 = ^{(5 * 12)}/₈ = ⁶⁰/₈ = ³⁰/₄ = ¹⁵/₂ = 7¹/_2.

svaret: 7¹/_2.

Som det kan sees fra det foregående eksempel, var det nødvendig å redusere det resulterende utfall og konvertere uriktig fraksjonert uttrykk i den blandede tall.

Multiplikasjonen av fraksjoner gjelder også å finneprodukt av et tall i blandet form og en naturlig faktor. Hvis du vil multiplisere disse to tallene, multipliserer hele delen av den blandede faktoren med tallet, multipliserer telleren med samme verdi, og la nevneren være uendret. Hvis nødvendig, bør resultatet forenkles så mye som mulig.

eksempel. Finn produktet 9⁵/₆ og 9.

Løsningen. 9⁵/₆ x 9 = 9 x 9 + ^{(5 x 9)}/₆ = 81 + ⁴⁵/₆ = 81 + 7³/₆ = 88¹/_2.

svaret: 88¹/_2.

Multiplikasjon med faktorer på 10, 100, 1000 eller 0,1; 0,01; 0001

Den foregående regelen innebærer følgende. For å multiplisere en desimalfraksjon med 10, 100, 1000, 10000, etc., flytt kommaet til høyre med så mange sifre i sifrene som det er nuller i multiplikatoren etter en.

Eksempel 1. Finn produktet av 0,065 og 1000.

Løsningen. 0,065 x 1000 = 0065 = 65.

svaret: 65.

Eksempel 2. Finn produktet 3,9 og 1000.

Løsningen. 3,9 x 1000 = 3,900 x 1000 = 3900.

svaret: 3900.

Hvis det er nødvendig å multiplisere det naturlige tallet og 0,1;0,01; 0,001; 0,0001 og så videre. E., bør være beveget til venstre et komma i det resulterende produkt i like mange siffer symboler som nuller er til enhet. Om nødvendig er nuller skrevet foran det naturlige nummeret i tilstrekkelig mengde.

Eksempel 1. Finn produktet av 56 og 0.01.

Løsningen. 56 x 0,01 = 0056 = 0,56.

svaret: 0,56.

Eksempel 2. Finn produktet 4 og 0,001.

Løsningen. 4 x 0,001 = 0004 = 0,004.

svaret: 0,004.

Så å finne produktet av forskjellige fraksjoner skal ikke forårsake vanskeligheter, bortsett fra at beregningen av resultatet; i dette tilfellet kan du ikke gjøre uten kalkulator.