Slik finner du minimum og maksimum poeng for en funksjon: funksjoner, metoder og eksempler

Funksjon og studie av dens funksjoner taret av nøkkelkapitlene i moderne matematikk. Hovedkomponenten i en hvilken som helst funksjon er grafer som representerer ikke bare dens egenskaper, men også parametrene for derivatet av denne funksjonen. La oss se på dette vanskelige emnet. Så, hvor best å finne maksimal og minimum poeng av funksjonen?

Funksjon: Definisjon

Enhver variabel som avhenger av verdien av en annen mengde, kan kalles en funksjon. For eksempel, funksjonen f (x²) er kvadratisk og bestemmer verdiene for hele settet x. Anta at x = 9, da verdien av vår funksjon vil være 9²= 81.

Funksjoner kan være av alle slag: logisk, vektor, logaritmisk, trigonometrisk, numerisk og andre. De studerte slike fremragende sinn som Lacroix, Lagrange, Leibniz og Bernoulli. Deres arbeid tjener som et høyborg på moderne måter å studere funksjoner på. Før du finner minimumspunkter, er det svært viktig å forstå selve betydningen av funksjonen og dens derivat.

Derivat og dets rolle

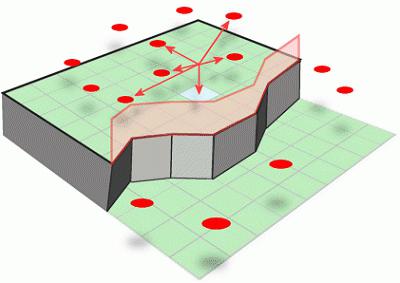
Alle funksjoner er avhengige av deresvariabler, noe som betyr at de kan endre verdien sin når som helst. På grafen vil dette bli representert som en kurve, som deretter slippes, stiger deretter langs ordinaten (dette er hele settet med tallene "y" langs grafenes vertikal). Så definisjonen av punktet med maksimum og minimum av funksjonen er bare relatert til disse "fluktuasjonene". Vi vil forklare hva dette forholdet er.

Derivatet av en hvilken som helst funksjon er tegnet på grafenmed det formål å studere hovedtrekkene sine og beregne hvor raskt funksjonen endres (det vil si det endrer verdien avhengig av variabelen "x"). I dette øyeblikk, når funksjonen øker, grafen over dets derivat vil også øke, men ved en hvilken som helst annen funksjon kan begynne å avta, og deretter grafen av derivatet vil avta. Poengene der derivatet går fra minustegnet til plustegnet, kalles minimumspunkter. For å vite hvordan du finner minimumspunkene, bør du bedre forstå begrepet derivatet.

Hvordan beregne derivatet?

Definisjon og beregning av derivatet av en funksjoninnebærer flere begreper fra differensialkalkulatoren. Generelt kan selve definisjonen av derivatet uttrykkes som følger: Dette er verdien som angir hastigheten på endringen av funksjonen.

En matematisk måte å definere den for mangeelevene virker kompliserte, men faktisk er alt mye enklere. Det er bare nødvendig å følge standardplanen for å finne avledet av en hvilken som helst funksjon. Nedenfor beskriver vi hvordan du kan finne minimumspunktet til en funksjon uten å anvende differensieringsregler og uten å lære tabellen over derivater.

1. Derivatet av en funksjon kan beregnes ved bruk avgrafikk. For å gjøre dette må du representere selve funksjonen, og ta et enkelt punkt på det (punkt A i fig.). Vertikalt nedover tegner du en linje til abscissen-aksen (punktet x₀), og ved punktet A tegner du en tangent til grafenfunksjon. Abscissen og tangensaksen danner en vinkel a. For å beregne verdien av hvor raskt funksjonen vokser, er det nødvendig å beregne tangenten til denne vinkelen a.
2. Det viser seg at tangentet til vinkelen mellom tangent ogX-aksens retning er derivatet av funksjonen på en liten del med punkt A. Denne metoden anses som en geometrisk måte å bestemme derivatet på.

Metoder for å undersøke funksjonen

I skolen matematikk programmet er det muligfinne minimumspunktet til en funksjon på to måter. Den første metoden ved hjelp av grafen vi allerede demonterte, men hvordan bestemmer vi den numeriske verdien av derivatet? For å gjøre dette må du lære noen formler som beskriver egenskapene til derivatet og hjelpe konvertere variabler av typen "x" til tall. Følgende metode er universell, så den kan brukes på nesten alle typer funksjoner (både geometrisk og logaritmisk).

1. Det er nødvendig å likestille funksjonen med derivatfunksjonen, og deretter forenkle uttrykket ved hjelp av differensieringsreglene.
2. I noen tilfeller, når en funksjon er gitt, isom variabelen "x" er i divisoren, er det nødvendig å bestemme rekkevidden av tillatte verdier, unntatt punktet "0" fra det (av den enkle grunnen som i matte i intet tilfelle kan deles inn i null).
3. Etter dette er det nødvendig å forvandle den opprinnelige formen til funksjonen til en enkel likning, som tilsvarer hele uttrykket til null. For eksempel, hvis funksjonen så slik ut: f (x) = 2x³+ 38x, deretter ved differensieringsreglene er dens derivat lik f "(x) = 3x²1. Da forvandler vi dette uttrykket til en ligning med følgende form: 3x²+1 = 0.
4. Etter å ha løst ligningen og funnet poengene "x"det er nødvendig å skildre dem på abscissen akse og avgjøre om derivatet i disse seksjonene mellom de markerte punktene er positivt eller negativt. Etter notasjonen blir det klart på hvilket tidspunkt funksjonen begynner å redusere, det vil si, det endrer skiltet fra negativt til negativt. På denne måten finner du både minimum og maksimum poeng.

Differensieringsregler

Den mest grunnleggende komponenten i studien av funksjonen udets derivat er kjennskap til regler for differensiering. Bare med deres hjelp kan du konvertere tungvint uttrykk og store komplekse funksjoner. La oss bli kjent med dem, det er mange av dem, men de er alle veldig enkle på grunn av de vanlige egenskapene til både kraft og logaritmiske funksjoner.

1. Derivatet av enhver konstant er lik null (f (x) = 0). Det vil si at derivatet f (x) = x⁵+ x - 160 vil ha formen: f "(x) = 5x⁴1.
2. Derivatet av summen av to termer: (f + w) "= f" w + fw ".
3. Derivatet av logaritmisk funksjon: (log_end) "= d / ln a * d Denne formelen gjelder for alle typer logaritmer.
4. Derivat av grad: (xⁿ) "= n * x^n-1. For eksempel (9x²) "= 9 * 2x = 18x.
5. Derivatet av sinusformet funksjon: (sin a) "= cos a. Hvis synden av vinkelen a er 0,5, er dens derivat lik √3 / 2.

Ekstreme poeng

Vi har allerede sortert ut hvordan du finner minimumspunkene,Imidlertid er det et konsept av maksimalpoengene til en funksjon. Hvis minimum representerer de punkter hvor funksjonen forløper med minustegnet til en pluss den maksimale punktene er de punkter på x-aksen ved hvilken den deriverte skifter fra pluss-funksjon på motsatt - minus.

Du kan finne maksimalpoengene i henhold til den ovenfor beskrevne metoden, men du bør merke at de angir de delene som funksjonen begynner å redusere, det vil si at derivatet vil være mindre enn null.

I matematikk er det vanlig å generalisere begge konsepter,erstatte dem med uttrykket "extremum poeng". Når en jobb blir bedt om å bestemme disse punktene, betyr det at det er nødvendig å beregne derivatet av en gitt funksjon og finne minimum og maksimum poeng.